Hackaton Report - Code Review

Author

Anthony Tricarico

1 Introduction

Understanding to what extent the results of a Large Language Model (LLM) can be trusted in text generation tasks is of fundamental importance nowadays. To this end, this technical report discusses the results of an experiment carried out using an open source LLM (Mistral) to understand how well this kind of model can represent the emotional context conveyed through a textual prompt. Mistral’s model was instructed to generate texts following a prompt that could be either positively or negatively charged emotionally. Moreover, the temperature of the model was also manipulated to check for possible drifts from the given prompts with higher temperatures. The results of a semantic frame analysis are reported to show that the emotions that occur in an LLM-generated text are mostly in line with the expectations provided by the content of the prompt used to generate the text. Additional analyses are discussed to quantify semantical and logical correctness to show that open source LLMs perform very well for the task considered in the current experiment but are not immune to biases.

This additional portion of the report goes through the technical steps and setup of the code used to produce the data and analyze it.

2 Generating data

Data for this experiment was produced in two steps. During the first iteration, carried out calling the API remotely, we asked the API to produce the entire sample of data (around 600 texts, 200 for each temperature level selected). However, we noticed that most of the texts produced with the highest temperature (1.3) were not usable and after cleaning them (in Python using the clean_data.py script) we had to rebalance the groups and adjust for the dropped texts from the highest temperature group.

#! clean_data.py

# function used to clean the data
def clean_df(df: pd.DataFrame) -> pd.DataFrame:

    # make text lowercase
    df['text_lower'] = df['text'].str.lower()

    # drop if text is shorter than 500 characters
    min_length = df['text_lower'].str.len() >= 500
    
    # check if text starts with parenthesis
    parenthesis = df['text_lower'].str.startswith('(')
    
    # check if non ascii letters are used
    non_ascii_mask = df['text'].apply(lambda x: not all(ord(char) < 128 for char in str(x)))

    df_cleaned = df[(~parenthesis) & (~non_ascii_mask) & (min_length)]

    return df_cleaned

To this end, the second iteration of the text generation happened. This time, however, the same Mistral model was run locally using the framework provided by ollama and exploiting the connection to the locally hosted API. The texts produced in this fashion passed all cleaning tests and were included in the final dataset by running the clean_data.py script and saving the final merged dataset in .csv format. The last step was to compute \(z\)-scores for each emotion embedded in the generated texts using the create_emotions_df.py script. The final dataset (emotions.csv) was then saved and was used for the subsequent analyses. After performing this step, no more data cleaning was needed.

from emoatlas import EmoScores
import pandas as pd

# compute emotion scores
def compute_scores(df: pd.DataFrame, n = -1):
    emos = EmoScores()
    
    # initialize empty dictionary to store the scores
    dct = {
      'anger' : list(),
      'trust' : list(),
      'surprise' : list(), 
      'disgust' : list(),
      'joy' : list(),
      'sadness' : list(),
      'fear' : list(),
      'anticipation' : list()
    }

    # compute score for each text in the df
    for i in range(len(df)):
        text = df['text'].iloc[i]
        # compute emotional scores using EmoAtlas
        scores = emos.zscores(text)
        # append to each emotion the score for the current text
        for k in scores:
            dct[k].append(scores[k])

    return dct

3 Experiment 1 - Statistical Analysis

The analysis for the first study was carried out using R version 4.4.3 and the following packages:

Code 
library(pacman)
p_load(tidyverse, ggplot2, readr, janitor, psych, ggthemes, car, stringr ,rstatix, patchwork, gridExtra, gt)
theme_set(theme_minimal())

Data was then imported:

Code 
emotions <- read_csv("generated_data/cleaned/emotions.csv")
# remove first two columns, keep all others
emotions <- emotions[, 3:length(emotions)]

3.1 Data pre-processing

The first step in preparing this analysis is to declare the groups and specify their partitioning in the dataframe.

Then, it is informative to look at different summary statistics for each condition.

Code 
# check summary statistics by condition
describeBy(emotions ~ condition)

3.2 Assumption checks for ANOVA

When comparing multiple means, the first test that comes to mind is ANOVA. However, since it is a parametric test, it is important to check if the assumption that it makes on data are respected. The two main assumptions of ANOVA are:

  1. The dependent variable is normally distributed across groups
  2. The dependent variable shares the same variance across groups

To check those assumptions, two tests are usually employed: Shapiro-Wilk’s test, and Levene’s test. If any one of those tests returns a statistically significant result for any emotion, then it means that ANOVA cannot be used as the data violates the basic assumptions that it makes. A level of significance \(\alpha\) of 5% is used to interpret statistical significance for those tests.

Below follows a summary of the results from the tests:

Levene's Test for Homogeneity of Variance by Emotion
Emotion F Value df1 df2 p-value Equal Variance?
anger 0.71 5 584 0.6183 Yes
trust 0.25 5 584 0.9373 Yes
surprise 3.06 5 584 0.0098 No
disgust 0.82 5 584 0.5368 Yes
joy 3.39 5 584 0.0050 No
sadness 0.94 5 584 0.4533 Yes
fear 2.37 5 584 0.0380 No
anticipation 4.13 5 584 0.0011 No
Shapiro-Wilk Test for Normality by Emotion and Condition
Emotion Condition p-value Normal?
anger n+0.1 0.2004 Yes
anger n+0.7 0.1641 Yes
anger n+1.3 0.0208 No
anger p+0.1 0.1618 Yes
anger p+0.7 0.6195 Yes
anger p+1.3 0.3423 Yes
trust n+0.1 0.9100 Yes
trust n+0.7 0.4335 Yes
trust n+1.3 0.0666 Yes
trust p+0.1 0.1463 Yes
trust p+0.7 0.4301 Yes
trust p+1.3 0.1031 Yes
surprise n+0.1 0.3537 Yes
surprise n+0.7 0.9749 Yes
surprise n+1.3 0.5589 Yes
surprise p+0.1 0.6126 Yes
surprise p+0.7 0.1008 Yes
surprise p+1.3 0.9456 Yes
disgust n+0.1 0.0060 No
disgust n+0.7 0.0032 No
disgust n+1.3 0.0841 Yes
disgust p+0.1 0.0465 No
disgust p+0.7 0.0319 No
disgust p+1.3 0.3060 Yes
joy n+0.1 0.0414 No
joy n+0.7 0.3174 Yes
joy n+1.3 0.9608 Yes
joy p+0.1 0.3646 Yes
joy p+0.7 0.2609 Yes
joy p+1.3 0.3918 Yes
sadness n+0.1 0.1759 Yes
sadness n+0.7 0.2254 Yes
sadness n+1.3 0.0620 Yes
sadness p+0.1 0.0013 No
sadness p+0.7 0.6058 Yes
sadness p+1.3 0.8476 Yes
fear n+0.1 0.3349 Yes
fear n+0.7 0.4868 Yes
fear n+1.3 0.2285 Yes
fear p+0.1 0.5988 Yes
fear p+0.7 0.5448 Yes
fear p+1.3 0.1645 Yes
anticipation n+0.1 0.4075 Yes
anticipation n+0.7 0.7328 Yes
anticipation n+1.3 0.6227 Yes
anticipation p+0.1 0.6037 Yes
anticipation p+0.7 0.9497 Yes
anticipation p+1.3 0.9065 Yes

As it is possible to observe these departures from the assumptions it becomes necessary to use non-parametric alternatives to the ANOVA test.

3.3 Kruskal-Wallis Test

This is an alternative to the ANOVA test and can be used for this specific dataset. As in the ANOVA test if the null hypothesis is rejected, then we know at least one group is different on average compared to another. The results for this test are reported below.

Kruskal-Wallis Test Results by Emotion
Emotion Chi-squared df p-value Significant Difference?
anger 38.31 5 0.0000 Yes
trust 2.40 5 0.7921 No
surprise 15.62 5 0.0080 Yes
disgust 17.59 5 0.0035 Yes
joy 217.66 5 0.0000 Yes
sadness 287.76 5 0.0000 Yes
fear 143.33 5 0.0000 Yes
anticipation 114.40 5 0.0000 Yes

Then similarly to ANOVA, also this test needs to be followed up by a post-hoc which in this case is represented by the t-test non-parametric counterpart: Dunn’s test.

3.3.1 Dunn’s test as post-hoc follow up

Code 
# only one significant difference between p+0.7 and p+1.3
dunn_test(emotions, surprise~condition,
                     p.adjust.method = "BH")
# evidence of some difference in disgust between negative and positive prompt
dunn_test(emotions, disgust~condition,
          p.adjust.method = "BH")
# clear-cut difference in joy between negative and positive prompt
dunn_test(emotions, joy~condition,
          p.adjust.method = "BH")
# clear-cut difference in sadness between negative and positive prompt
dunn_test(emotions, sadness~condition,
          p.adjust.method = "BH")
# clear-cut difference in fear between negative and positive prompt
dunn_test(emotions, fear~condition,
          p.adjust.method = "BH")
# clear-cut difference in anticipation between negative and positive prompt
dunn_test(emotions, anticipation~condition,
          p.adjust.method = "BH")
Dunn Test (BH-adjusted) for Pairwise Comparisons by Emotion
Emotion Group 1 Group 2 Adjusted p-value Significance Code Significant?
surprise n+0.1 n+0.7 0.2472 ns No
surprise n+0.1 n+1.3 0.2797 ns No
surprise n+0.1 p+0.1 0.9533 ns No
surprise n+0.1 p+0.7 0.3607 ns No
surprise n+0.1 p+1.3 0.0553 ns No
surprise n+0.7 n+1.3 0.9396 ns No
surprise n+0.7 p+0.1 0.2472 ns No
surprise n+0.7 p+0.7 0.0553 ns No
surprise n+0.7 p+1.3 0.3439 ns No
surprise n+1.3 p+0.1 0.2797 ns No
surprise n+1.3 p+0.7 0.0798 ns No
surprise n+1.3 p+1.3 0.4315 ns No
surprise p+0.1 p+0.7 0.3621 ns No
surprise p+0.1 p+1.3 0.0553 ns No
surprise p+0.7 p+1.3 0.0168 * Yes
disgust n+0.1 n+0.7 0.8890 ns No
disgust n+0.1 n+1.3 0.8890 ns No
disgust n+0.1 p+0.1 0.0244 * Yes
disgust n+0.1 p+0.7 0.0244 * Yes
disgust n+0.1 p+1.3 0.3199 ns No
disgust n+0.7 n+1.3 0.8890 ns No
disgust n+0.7 p+0.1 0.0248 * Yes
disgust n+0.7 p+0.7 0.0248 * Yes
disgust n+0.7 p+1.3 0.3668 ns No
disgust n+1.3 p+0.1 0.1264 ns No
disgust n+1.3 p+0.7 0.1264 ns No
disgust n+1.3 p+1.3 0.5542 ns No
disgust p+0.1 p+0.7 0.8890 ns No
disgust p+0.1 p+1.3 0.5770 ns No
disgust p+0.7 p+1.3 0.5556 ns No
joy n+0.1 n+0.7 0.1836 ns No
joy n+0.1 n+1.3 0.0530 ns No
joy n+0.1 p+0.1 0.0000 **** Yes
joy n+0.1 p+0.7 0.0000 **** Yes
joy n+0.1 p+1.3 0.0000 **** Yes
joy n+0.7 n+1.3 0.3763 ns No
joy n+0.7 p+0.1 0.0000 **** Yes
joy n+0.7 p+0.7 0.0000 **** Yes
joy n+0.7 p+1.3 0.0000 **** Yes
joy n+1.3 p+0.1 0.0000 **** Yes
joy n+1.3 p+0.7 0.0000 **** Yes
joy n+1.3 p+1.3 0.0000 **** Yes
joy p+0.1 p+0.7 0.2060 ns No
joy p+0.1 p+1.3 0.2671 ns No
joy p+0.7 p+1.3 0.9155 ns No
sadness n+0.1 n+0.7 0.8573 ns No
sadness n+0.1 n+1.3 0.2224 ns No
sadness n+0.1 p+0.1 0.0000 **** Yes
sadness n+0.1 p+0.7 0.0000 **** Yes
sadness n+0.1 p+1.3 0.0000 **** Yes
sadness n+0.7 n+1.3 0.2954 ns No
sadness n+0.7 p+0.1 0.0000 **** Yes
sadness n+0.7 p+0.7 0.0000 **** Yes
sadness n+0.7 p+1.3 0.0000 **** Yes
sadness n+1.3 p+0.1 0.0000 **** Yes
sadness n+1.3 p+0.7 0.0000 **** Yes
sadness n+1.3 p+1.3 0.0000 **** Yes
sadness p+0.1 p+0.7 0.6706 ns No
sadness p+0.1 p+1.3 0.7484 ns No
sadness p+0.7 p+1.3 0.9775 ns No
fear n+0.1 n+0.7 0.4121 ns No
fear n+0.1 n+1.3 0.9906 ns No
fear n+0.1 p+0.1 0.0000 **** Yes
fear n+0.1 p+0.7 0.0000 **** Yes
fear n+0.1 p+1.3 0.0001 **** Yes
fear n+0.7 n+1.3 0.5157 ns No
fear n+0.7 p+0.1 0.0000 **** Yes
fear n+0.7 p+0.7 0.0000 **** Yes
fear n+0.7 p+1.3 0.0000 **** Yes
fear n+1.3 p+0.1 0.0000 **** Yes
fear n+1.3 p+0.7 0.0000 **** Yes
fear n+1.3 p+1.3 0.0009 *** Yes
fear p+0.1 p+0.7 0.6706 ns No
fear p+0.1 p+1.3 0.0776 ns No
fear p+0.7 p+1.3 0.1692 ns No
anticipation n+0.1 n+0.7 0.6813 ns No
anticipation n+0.1 n+1.3 0.5507 ns No
anticipation n+0.1 p+0.1 0.0000 **** Yes
anticipation n+0.1 p+0.7 0.0000 **** Yes
anticipation n+0.1 p+1.3 0.0000 **** Yes
anticipation n+0.7 n+1.3 0.3577 ns No
anticipation n+0.7 p+0.1 0.0000 **** Yes
anticipation n+0.7 p+0.7 0.0000 **** Yes
anticipation n+0.7 p+1.3 0.0000 **** Yes
anticipation n+1.3 p+0.1 0.0001 *** Yes
anticipation n+1.3 p+0.7 0.0000 **** Yes
anticipation n+1.3 p+1.3 0.0013 ** Yes
anticipation p+0.1 p+0.7 0.1629 ns No
anticipation p+0.1 p+1.3 0.9822 ns No
anticipation p+0.7 p+1.3 0.2837 ns No

Apart from surprise and disgust, we can see that all other emotions present a clear-cut difference between negative and positive prompts.

4 Experiment 2

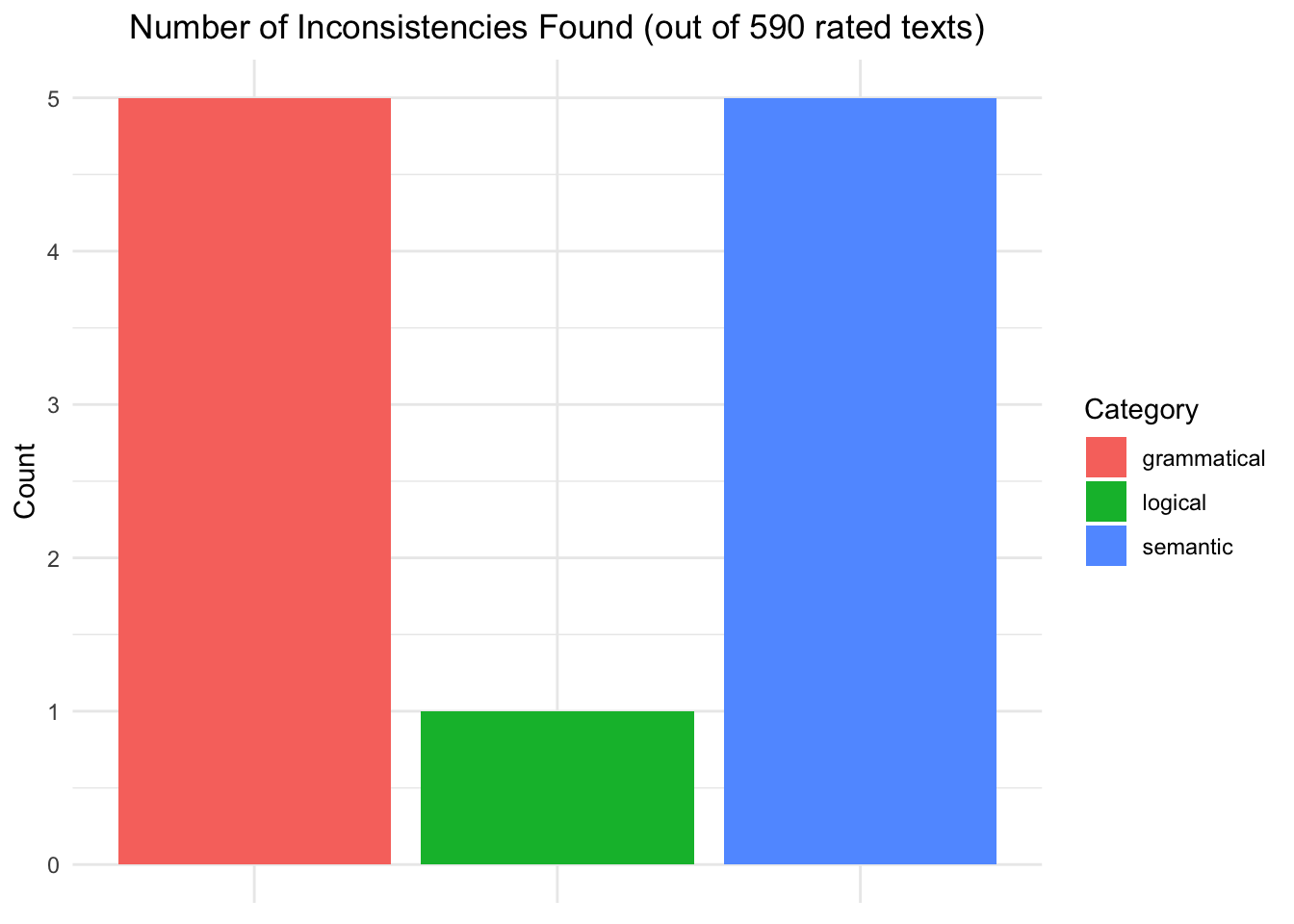
A second experiment was proposed to find whether semantical or logical inconsistencies were present in the generated texts and were causing this imbalance. To do this, Google’s Gemma3 model was used as an annotator and instructed via a specific prompt to detect the aforementioned inconsistencies in the texts. The results indicate that almost none of the texts rated by the annotator model included inconsistencies with a total of only five texts containing semantical inconsistencies (around 0.8% of all considered instances).

To set up this experiment and try it a few steps need to be carried out:

  1. set up Factgenie by referring to the official documentation available at https://github.com/ufal/factgenie

  2. run the make_jsonl_input.py and make_jsonl_output.py to prepare data for the analysis inside of the self-hosted web app offered by Factgenie

  3. start up the app by running the following in a CLI instance:

    factgenie run --host=127.0.0.1 --port 8890

    When inside the app we imported the data as instructed in the app setup by separating instances of prompts used to generate the texts from the outputs (i.e., the two .jsonl files generated in step 2.

Gemma3 wrote the annotations and showed that only 5 texts out of 590 showed semantical inconsistencies. The results are available in the llm-eval-gemini27B.csv file.

Code 
# import dataset with LLM annotations and evaluations
llm_eval_gemini27B <- read_csv("generated_data/llm-evals/llm-eval-gemini27B.csv")
Code 
ggplot(llm_eval_gemini27B, aes(x = Category, y = Count, fill = Category)) +
  geom_col() +
  labs(title = "Number of Inconsistencies Found (out of 590 rated texts)") +
  theme(plot.title = element_text(hjust = 0.5),
        axis.text.x = element_blank(),
        axis.title.x = element_blank())